Homework 4
MATH 301/601
Test #4 is on Wednesday, April 2
 

Instructions. Read the Homework Guide to make sure you understand how to successfully complete the assignment. Click here for a pdf version of the homework.

Exercise 1.

In Section 5.4 of the textbook, complete exercises 1, 2(a,b,c,d), and 4.

Exercise 2.

Determine if each of the following subsets of $S_4$ is a subgroup or not.

1. $\{\sigma \in S_4:\sigma (1)=3\}$

2. $\{\sigma \in S_4:\sigma (2)=2\}$

3. $\{\sigma \in S_4:\sigma (\{2,3\})=\{2,3\}\}$

Exercise 3.

Prove that the order of $S_n$ is $n!$ (recall that $n!=n(n-1)(n-2)\mathrm{\cdots }2\cdot 1$).

*Exercise 4.

Choose examples of 2-, 3-, 4-, and 5-cycles, and compute the cyclic subgroups they generate. Use these examples to conjecture the order of a $k$-cycle. Prove your conjecture.

*Exercise 5.

A 2-cycle is called a transposition. Prove that a $k$-cycle can be expressed as a product of $k-1$ transpositions.

Exercise 6.

For $n\ge 3$, prove that the center of $S_n$ is trivial (that is, it only contains the identity element).

Exercise 7.

Let $\sigma$ be a $k$-cycle. Prove that $k$ is odd if and only if ${\sigma }^2$ is a cycle.

**Exercise 8.

***Oops***: This is the same as Exercise 16, but Exercise 16 is more scaffolded, so just do that one. Prove that any two $k$-cycles in $S_n$ are conjugate, that is, if $\sigma ,\tau \in S_n$ are $k$-cycles, then there exists $\mu \in S_n$ such that $\mu \sigma {\mu }^{-1}=\tau$.

Exercise 9.

What are the possible cycle structures of elements in $A_5$? What about $A_6$?

*Exercise 10.

Prove that in $A_n$ with $n\ge 3$, any permutation is a product of cycles of length 3.

Figure 1: A tetrahedron with vertices labelled.

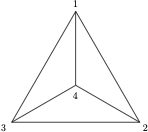
**Exercise 11.

Label the vertices of a tetradhedron by 1, 2, 3, and 4 (see Figure 1). For each of the permutations $(\mathrm{1\hspace{0.17em}2\hspace{0.17em}3})$ and $(12)(34)$ in $A_4$, describe a rigid motion of the tetrahedron that induces the permutation.

Exercise 12.

A series of questions dealing with cycles decompositions and orders.

1. Find all possible orders of elements in $S_7$.

2. Find all possible orders of elements in $A_7$.

3. Show that $A_{10}$ contains an element of order 15.

4. Does $A_8$ contain an element of order 26?

5. What are the possible cycle decomposition structures of elements in $A_5$? What about $A_6$?

*Exercise 13.

The goal of this exercise is to deduce the order of the alternating group $A_n$ for $n\in \mathbb{N}$. Throughout the exercise, let $B_n$ be the subset of $S_n$ consisting of odd permutations (recall that $A_n$ is the subgroup of $S_n$ consisting of even permutations).

1. Prove that $A_n\cap B_n=\mathrm{\varnothing }$.

2. Fix $\tau \in B_n$, and define $f:A_n\to B_n$ by $f(\sigma )=\tau \sigma$. Prove that $f$ is a bijection.

3. Use the previous parts, together with the facts that $S_n=A_n\cup B_n$ and $|S_n|=n!$, to deducde that $|A_n|=\frac{n!}{2}$.

*Exercise 14.

Let $n\in \mathbb{N}$. Prove that in $A_n$ with $n\ge 3$, any permutation is a product of 3-cycles.

*Exercise 15.

This exercises provides a more formal approach to a problem you worked on on an earlier homework. Let $\mathrm{\Gamma }=(V,E)$ be the graph with $V=\mathbb{Z}$ and $(m,n)\in \mathbb{Z}$ if and only if $|m-n|=1$. So, $\mathrm{\Gamma }$ is just the number line (a portion of which is drawn here):

The infinite dihedral group, denoted $D_{\mathrm{\infty }}$, is the automorphism group of the graph $\mathrm{\Gamma }$. Let $\tau ,\rho \in D_{\mathrm{\infty }}$ be given by $\tau (n)=n+1$ and $\rho (n)=-n$ for $n\in \mathbb{Z}$.

1. For $k\in \mathbb{Z}$, write down a formula for ${\tau }^k$.

2. Prove that if $f\in D_{\mathrm{\infty }}$ such that $f(0)=0$ and $f(1)=1$, then $f$ is the identity. (Hint: Let’s first focus on the natural numbers. Use strong induction: Let $k\in \mathbb{N}\setminus \{1\}$. Suppose that $f(j)=j$ for all and prove that $f(k)=k$. A similar argument works for the negative integers.)

3. Prove that every element of $D_{\mathrm{\infty }}$ can be written as either ${\tau }^k$ or ${\tau }^k\rho$ for some $k\in \mathbb{Z}$. (Hint: let $f\in D_{\mathrm{\infty }}$. Use a power of $\tau$ to get $f(0)$ back to $0$, and then use $\rho$ to get 1 back to itself if necessary.)

**Exercise 16.

Let $\tau =(a_1{a}_2\mathrm{\dots },a_k)$ be a $k$-cycle.

1. Prove that if $\sigma$ is any permutation, then

   $$\sigma \tau {\sigma }^{-1}=(\sigma (a_1)\sigma (a_2)\mathrm{\dots }\sigma (a_k))$$

   is a $k$-cycle.

2. Let $\mu$ be a $k$-cycle. Prove that there is a permutation $\sigma$ such that $\sigma \tau {\sigma }^{-1}=\mu$.